A. Pengertian Bentuk Aljabar
x, 2y, x+3y , 3p+5q, a² + b + 3 disebut bentuk aljabar
ax²+ bx + c = 0 ; a,b,c,x dan 0 adalah lambang-lambang aljabar a dan b disebut
koefisien ; c disebut konstanta ; x² dan x disebut variabel
2x²; 2 disebut koefisien dan x² disebut variabel
5q ; 5 disebut koefisien dan q disebut variabel
2x dan 3x merupakan dua suku sejenis
x² dan 7 x merupakan dua suku tidak sejenis
B. Operasi Pada Bentuk Aljabar
1. Penjumlahan dan Pengurangan
Suku-suku yang dapat dijumlahan/dikurangkan adalah suku-suku yang sejenis,
yang dijumlahkan/dikurangkan adalah koefisiennya
a. Penjumlahan
ax + bx = (a+b)x
ax + b + cx + d = (a+c)x + (b+d)
contoh:
7x + 3x = ?
7x + 3x = (7+3)x = 10x
2x² - 3 x² = ?
x² - 3x² = (-2-3) x² = - 5x²
2 x² -3 + x² - 4 = ?
2 x² -3 + x² - 4 = (2+1) x² + (-3-4) = 3 x² - 7
b. Pengurangan
ax - bx = (a-b)x
ax - b - cx - d = (a - c)x - (b+d)
contoh :
7x – 3x = ?
7x – 3x = (7-3)x = 4x
5x – 8 – 2x – 1 = ?
5x – 8 – 2x – 1 = (5-2)x – (8+1) = 3x – 9
2. Perkalian dan Pembagian
- Perkalian
a. Perkalian konstanta dengan bentuk aljabar
a(bx+cy) = abx + acy
contoh :
5 (2x+4y) = 10x + 20y
-3(3x-2y) = -9x + 6y
b. Perkalian bentuk aljabar dengan bentuk aljabar
ax(bx+cy) = abx² + acxy
ay(bx+cy) = abxy + acy²
(x+a) (x+b) = x² + bx + ax +ab
contoh :
3x(2x+3y) = 6 x² + 9xy
(3x+y) (x-2y) = 3 x . x + (3x . -2y) + y. x + (y . -2y)
= 3 x² + (-6xy)+xy+(-2y²)
= 3x² - 5xy – 2y²
- Pembagian
Contoh:
3. Pemangkatan
Sifat-sifat pemangkatan bilangan bulat berlaku juga pada pemangkatan bentuk
aljabar.
Contoh:
(3x)² = 3x . 3x
= 9x²
(2xy)² = 2xy . 2xy
= 4x²y²
a. Pemangkatan bentuk aljabar dalam bentuk x + y
contoh:
(x + y)²= (x+y) (x+y)
= (x+y) x + (x+y) y
= x² + xy + xy + y²
= x² + 2xy + y²
b.Pemangkatan bentuk aljabar dalam bentuk x - y
contoh:
(x - y)²= (x - y) (x - y)
= (x- y) x - (x - y) y
= x²- xy - xy + y²
= x²- 2xy + y²
Pemangkatan bentuk-bentuk aljabar dapat dilakukan dengan menggunakan
kaidah Segitiga Pascal sbb:
dan seterusnya dan seterusnya
Perpangkatan bentuk aljabar (x-y)n dengan n bilangan asli juga menggunakan
kaidah Segitiga Pascal, akan tetapi tanda setiap koefisiennya berganti dari (+)
untuk suku ganjil dan (-) untuk suku genap.
dan seterusnya
4. Pemfaktoran
a. Bentuk distributif
ax ± ay = a (x ± y) ; a bisa koefisien atau variabel
contoh:
3x + 9y = 3 (x + 3y) ; a berbentuk koefisien
ax – ay = a (x – y) ; a berbentuk variabel
b. Selisih kuadrat
x² - y² = (x + y) ( x – y)
contoh:
x² - 4² = x² – 16 = (x + 4) (x – 4)
c. Kuadrat sempurna
x² + 2xy + y² = (x + y)²
x² - 2xy + y² = (x - y)²
contoh:
x² + 8x + 16 = (x + 4)²
x² – 8x + 16 = (x - 4)²
d. Bentuk ax2 + bx + c = 0 dimana a = 1
ax² + bx + c = (x + m) (x + n)
dengan m + n = b dan m.n = c
Contoh:
x² + 7x + 12 = (x + 4) ( x + 3)
m + n = 7 dan m . n = 12
yang memenuhi adalah m= 4 dan n= 3 atau m= 3 dan n= 4
e. Bentuk ax2 + bx + c = 0 dimana a ≠ 1
a. c = m. n dan m + n = b
Contoh:
2x2 + 3x + 1 = 0
2 . 1 = m . n dengan syarat m + n = 3
yang memenuhi adalah m = 2 dan n = 1 atau sebaliknya maka
2x² + 3x + 1 = 0 menjadi 2x² + 2x + x + 1 = 0
2x (x + 1) + 1 (x+1) = 0
(2x + 1 ) (x + 1)
C. Operasi Pecahan dalam Aljabar
Dalam Bentuk Aljabar juga dapat berupa pecahan
Contoh:
1. Penjumlahan dan Pengurangan
Konsep penjumlahan dan pengurangan pecahan dalam bentuk aljabar sama
dengan penjumlahan/pengurangan pecahan biasa yaitu dengan menyamakan penyebutnya terlebih dahulu.
Contoh:
2. Perkalian dan Pembagian
a. Perkalian
Pada perkalian bentuk pecahan penyelesaiannya dengan cara mengalikan
pembilang dengan pembilang dan penyebut dengan penyebut.
contoh:
b. Pembagian
Pada pembagian bentuk pecahan penyelesaiannya sama dengan bentuk pecahan biasa.
contoh:
D. Menyederhanakan Pecahan Bentuk Aljabar
Penyederhanaan pecahan bentuk aljabar dapat dilakukan dengan menggunakan
operasi bentuk aljabar. Faktorkan pembilang dan penyebut kemudian faktor yang
sama dari pembilang dan penyebut dibagi.
Contoh:
E. FPB dan KPK Bentuk Aljabar
Contoh:
Carilah FPB dan KPK dari bentuk: 2xy², 4xyz², 8x²yz
Jawab:
FPB ambil faktor yang sama dengan pangkat terkecil
KPK ambil semua faktor yang sama, pilih faktor dengan pangkat terbesar
2xy² = 2 . x . y²
4xyz² = 2² . x . y . z²
8x²yz = 2³ . x² . y . z
FPB = 2³ . x² . y² . z² = 8 x²y²z²
KPK = 2. x . y
BARISAN dan DERET
A. Pola Bilangan
Pola bilangan adalah aturan terbentuknya sebuah kelompok bilangan dengan suatu aturan yang telah diurutkan. Macam-macam pola bilangan dengan pola-pola tertentu sbb:
Barisan bilangan : 1,2,3,4,5,...
pola bilangan: n, n bilangan asli
Barisan bilangan: 2, 4, 6, 8, 10, ...
Pola bilangan: 2n, n bilangan asli
Barisan bilangan : 1,3,5,7,9,...
pola bilangan: 2n - 1, n bilangan asli
Barisan bilangan: 1, 4, 9, 16, ...
Pola bilangan: n2, n bilangan asli
Barisan bilangan : 1,3,6,10,...
pola bilangan: n (n + 1) , n bilangan asli
6. Bilangan persegipanjang
Barisan bilangan: 2, 6, 12, 20, ...
Pola bilangan: n (n+1), n bilangan asli
7. Bilangan Segitiga Pascal
Barisan bilangan : 1,2,,4,8,16, ...
pola bilangan: 2 n - 1 , n bilangan asli
Barisan bilangan adalah urutan suatu bilangan yang mempunyai aturan tertentu.
1. Barisan dan Deret Aritmetika
Barisan Aritmetika adalah suatu barisan bilangan dengan pola tertentu berupa
penjumlahan yang mempunyai beda (selisih) yang sama/tetap.
Suku-sukunya dinyatakan dengan:
a, a+ b, a+2b, a + 3b, ...., a + (n-1) b
Selisih(beda) dinyatakan dengan b:
b = U2 – U1 = U3 – U2 = Un – Un - 1
Suku ke n barisan aritmetika (Un) dinyatakan dengan rumus:
Un = suku ke n dengan n = 1,2,3, ...
a = suku pertama à U1 = a
Tentukan suku ke 15 barisan 2, 6, 10,14,...
Deret Aritmetika merupakan jumlah suku-suku pada barisan aritmetika.
Bentuk umum deret aritmetika:
a + (a + b) + (a+2b) + (a+3b) + ...+ (a+(n-1)b )
Jumlah suku sampai suku ke n pada barisan aritmetika dirumuskan dengan:
Sn = n/2 (2a + (n-1) b ) atau Sn = n/2 ( a + Un )
Suatu deret aritmetika 5, 15, 25, 35, ...
Berapa jumlah 10 suku pertama dari deret aritmetika tersebut?
b = 15 – 5 = 25 – 15 = 10
S10 = 10/2 ( 2. 5 + (10 -1) 10)
2. Barisan dan Deret Geometri
Barisan Geometri adalah suatu barisan bilangan dengan pola tertentu berupa
perkalian yang mempunyai rasio yang sama/tetap.
Suku-sukunya dinyatakan dengan:
Rasio dinyatakan dengan r :
Suku ke n barisan Geometri (Un) dinyatakan dengan rumus:
Un = suku ke n dengan n = 1,2,3, ...
a = suku pertama à U1 = a
Suku ke 10 dari barisan 2, 4, 8, 16, 32, ... adalah....
Deret Geometri merupakan jumlah suku-suku pada barisan geometri.
Bentuk umum deret geometri
Jumlah suku sampai suku ke n pada barisan geometri dirumuskan dengan:
Jika Rasio 0 < (r) < 1 :
Contoh soal:
Jumlah 7 suku pertama dari barisan 3, 9 , 27, ....
Jawab:
karena r > 1 maka menggunakan rumus
diketahui:
n = 7
a = 3
maka:
1. Pola titik di bawah ini menunjukkan barisan bilangan 1, 3, 6, 10,…..
Banyaknya titik pada suku ke 10 adalah….
pola bilangan = n/2 (n+1)
2. Diketahui barisan bilangan 2, 5, 8, 11, …., ....., maka Suku ke- (n +1) adalah…
3. Suatu jenis bakteri, setiap detik akan membelah diri menjadi dua.
Pada awalnya ada 5 bakteri, waktu yang diperlukan bakteri menjadi 320...
4. Diketahui suku ke-2 = 4 dan suku ke 8 = 16. Jumlah 10 suku pertama adalah..
Sn = n/2 (2a + (n – 1 ) b)
S10 = 10/2 (2 2 + (10 – 1 ) 2)
PERPANGKATAN dan AKAR
A. Pangkat Positif, Nol dan Negatif
Pangkat adalah salah satu operasi hitung.
Bentuk Umum:
contoh:
Sifat-sifat:
Contoh:
Sederhanakan bentuk
B. Pangkat Pecahan
Bilangan berpangkat pecahan dapat dinyatakan dalam bentuk:
Bentuk Akar:
Bentuk akar merupakan suatu bilangan positif di dalam pangkat pecahan
sifat-sifat bentuk akar:
Contoh:
Sederhanakan bentuk
Jawab:
C. Merasionalkan Bentuk Akar
Merasionalkan akar-akar yang bebentuk pecahan dapat diabuah dengan mengalikan akar-akar sekawannya.
1. Mengalikan pembilang dan penyebutnya dengan akar yang sama dengan penyebutnya.
Contoh:
Rasionalkan bentuk akar
Jawab:
2. Mengalikan pembilang dan pernyebutnya dengan akar sekawan dari penyebutnya
Penyebut 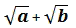 mempunyai sekawan
mempunyai sekawan 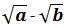
Penyebut 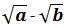 mempunyai sekawan
mempunyai sekawan 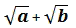
Contoh:
Rasionalkan bentuk akar
Jawab:
Latihan Soal Ulangan Harian dan Pembahasan
1. Sederhanakan:
Jawab:
2. Hitunglah nilai x dari:
Jawab:
3. Bakteri melakukan pembelahan dari 1 bakteri menjadi 254.
Berapa total waktu yang dibutuhkan jika setiap pembelahan membutuhkan waktu selama 2 menit?
Jawab:
Jadi waktu yang dibutuhkan = 2 menit x 8 = 16 menit
4. Jika a= 2, b =1/2 dan c=1,
Jawab:
5. Sederhanakanlah:
 Jawab:
Jawab:
6. Hasil dari:
7.  Jawab:
Jawab:
10. Bentuk sederhana dari:
Jawab












































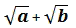 mempunyai sekawan
mempunyai sekawan 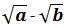
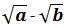 mempunyai sekawan
mempunyai sekawan